Using Op Amps to Interface to Spring-type Reverb Units
Although digital reverb units have achieved widespread use, the spring reverb is still popular in guitar amplifiers. Many such amplifiers use tubes for their sonic and overdrive characteristics, but for interfacing to a spring reverb, the monolithic op amp offers superior capabilities. This tech note, which discusses how to optimally interface a spring reverb to an op amp, is divided into three sections, one describing the drive circuit, another discussing the optimal drive level, and the final describing the signal-recovery circuit. In all sections, an Accutronics model 8DB2C1B or 8BB2C1B reverb unit is used as an illustrative example. The circuit design concepts presented here are equally applicable to other reverb units.
The Drive Amplifier
In a spring reverb, a solenoid (coil of wire) is used to generate a magnetic field that imparts vibrations to the unit's springs. As Ampere's Law shows, the strength of the field is proportional to the current through the coil, not the voltage across it. Yet, many reverb drive circuits produce a voltage rather than a current output. Why is this a problem? Well, the solenoid that produces the magnetic field is also an inductor, and the impedance of an inductor rises in direct proportion to the frequency applied to it. Therefore, given a constant voltage input, the current produced in, and the magnetic field produced by, the coil goes down in direct proportion to frequency. Mathematically, we can express this with a couple of simple equations:
![]()
where: zL = the coil's impedance
s = the complex frequency variable, j2p f
L = the coil's inductance
RL = the coil's resistance
Using Ohm's Law, we see that the current in the coil is:
![]()
So, using a voltage-output amplifier causes the reverb to produce less and less output as frequency goes up, which is not at all what one needs. It is the higher frequencies that produce a good reverb sound, and if the drive amp doesn't provide much output at these frequencies, the signal-recovery amp will need more gain and thus produce more noise.
Fortunately, a standard op amp allows an ideal solution to this dilemma. It is very simple and inexpensive to implement a current-output (technically speaking, a transconductance) amplifier with an op amp. The fact that the 8DBC1B's drive coil is not grounded makes the task especially easy. Consider the following circuit:
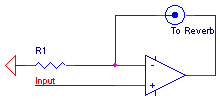
Any input voltage applied to the op amp's noninverting input appears at its inverting input as well. Thus, the current at the inverting node, and therefore through the reverb coil, is simply Vin/R1. So, we see that the circuit produces a current output in direct proportion to its voltage input. Two problems must be solved before the circuit is truly useful, however. First, we should roll off the stage's output at low frequencies, because they contribute nothing to the reverb sound; and second, as shown, this stage is unstable or marginally stable at best. To understand the cause of the instability, consider that through most of its frequency range, the op amp's open-loop transfer function produces a 90o phase shift. The network formed by the inductance of the reverb unit and R1 also produces a 90o phase shift, causing a total of 180o of phase shift around the feedback loop. The modifications shown in the circuit below solve both problems:
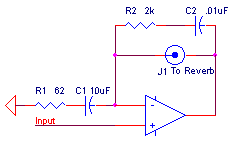
Capacitor C1 reduces the gain at low frequencies. Empirically, a 3 dB point for the R1, C1 network between 150 and 300 Hz seem about right. The test circuit uses a 62 ohm resistor for R1 and a 10 m F capacitor for C1. This combination produces a 3 dB point at about 260 Hz.
The network comprising C2 and R2 compensates the stage to make it stable. To see how, consider that at high frequencies, the inductive reactance of the reverb coil is high, and the capacitive reactance of C2 is low. Therefore, at high frequencies, R2 effectively becomes the feedback element, which restores phase margin to the circuit. To understand how to select R2 and C2, let's solve for the impedance, zf, of the feedback network formed by these two components and the reverb coil:
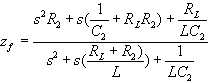
Looking at the denominator, we see it has the expected second-order form. To select C2, pick a frequency at which you would like the stage to break out of its rising feedback impedance to a constant one, using the standard formula:
![]()
A frequency between 5 kHz and 10 kHz is appropriate for a guitar amplifier. The 8DB2C1B tank has an inductance of about 44 mH; the test circuit uses a 0.01 m H capacitor to produce a break frequency of about 7.6 kHz.
Component R2 is selected to produce an appropriate Q according to the formula
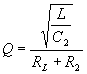
A 2 KW resistor should produce a Q of about 1, but core losses will lower the Q to that of a maximally-flat response. With these components, the magnitude of the feedback impedance is:
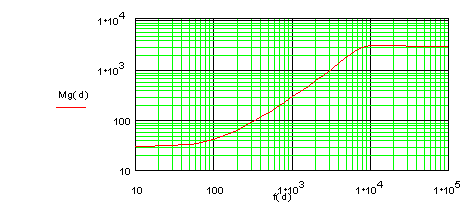
Next, we must look at the noise performance of this circuit. Several noise sources exist. First, let's consider the effect of op amp voltage noise (en). This noise source, which can range anywhere from 1 to 20 nV/rt. Hz for commonly available op amps, acts just like an input voltage. So, the current noise produced is simply en/R1. If we take a typical op amp noise of 5 nV/rt. Hz, this source causes output current noise of 0.08 nA/rt.Hz in the test circuit. The Johnson noise of R1 also contributes. The output current noise it produces is simply its Johnson noise divided by its resistance. For the test circuit, this noise is 0.016 nA/rt. Hz, which is 5 times lower than the noise caused by en. Therefore, we can ignore it. The Johnson noise of the reverb coil's resistance causes voltage noise at the output of the op amp, but no current noise, so it too can be ignored.
The current noise at the noninverting input of the op amp produces an input voltage that is simply the product of the current noise times the output impedance of the previous stage. This noise divided by R1 is the output noise from this source, so io = inRout/R1. If the previous stage had an output impedance of 20 kW , which is not uncommon for a tube stage, and if one used a bipolor-input op amp whose input current density were 1 pA/rt. Hz, which is typical of many such op amps, the output current noise would be about 0.3 nA/rt. Hz in the test circuit; this would be the dominant noise source. The lesson is clear: drive the stage from a low impedance or use a JFET-input op amp. Such amps typically have current noise densities of about 0.01 pA/rt. Hz. If either approach is taken, the noise from this source will be so low that it can be ignored. Op amp current noise at the inverting input simply goes into the reverb coil. This noise is also much lower than that caused by en, so it too can be ignored. Thus we see that in a properly designed stage, the op amp voltage noise is the only significant noise source.
What signal-to-noise ratios can be expected from such a stage? Let's say we choose an op amp whose voltage noise is 5 nV/rt. Hz, because such amps are cheap and easy to find. Let's assume a bandwidth of 10 kHz, which is conservative, because most guitar speakers don't produce much output beyond 5 or 6 kHz. Almost any op amp can put out 10 to 20 mA peak; let's be conservative again and assume that our stage can put out 7 mA rms. A quick calculation (peak rms output divided by the product of the noise density times the square root of bandwidth) shows a maximum signal-to-noise ratio of 119 dB!
Follow these simple design guidelines:
For good stability,
For low noise:
Designing For the Optimal Drive Level
Designing your drive amplifier so it can provide sufficient current to the reverb coil is a deceptively simple task. First, one must determine the optimal drive current that your particular model of reverb coil requires. Unfortunately, Accutronics' specifications can be a bit misleading. First, they publish a "nominal" drive level recommendation for their models. I'm not sure just what this number means, but I've concluded that it is best ignored. The number they provide that is meaningful is the maximum amp-turns that their drive coils can withstand before going into saturation. They spec this value as 25 amp-turns r.m.s.. Their use of an r.m.s. value here is also confusing, but let's assume they had sinusoidal excitation in mind, and therefore the peak current value would be 25*1.414 or about 35 amp-turns. I was able to verify by experiment that their drive coils (actually, of course, the cores of the coils) do go into saturation at about this level. So a design goal of a maximum drive level of about 30 amp-turns to allow for a safety factor seems about right.
To determine how much voltage we need to supply the reverb coil to produce current at this level, let's proceed simply and say that our guitar amp should be able to operate at full output up to 10 kHz. The 8DB2C1B's input coil has 688 turns and an impedance of 310 ohms at 1 kHz. So, at 10 kHz the required drive voltage is
![]()
A required drive level of 135 volts peak is not encouraging, but do we really need that much? Well, the highest note in a typical guitar is the D that is two octaves and a whole step above middle C. This note's frequency is 1175 Hz. In addition, a string that is fretted that high doesn't put out much power in its harmonics. To add to the good news, a guitar puts out maximum volume when a chord and not just a single string is played. By definition, all other notes in any chord containing the high D must be lower in frequency. So, for an undistorted guitar, the reverb doesn't need any more headroom than that required to reproduce a 1 kHz signal at full blast. For the subject reverb unit, we are only talking about a 13.5-volt peak signal.
13 volts is cutting things close for an ordinary op amp, so one might want to use a high-voltage op amp if a higher-voltage supply is available or switch to a lower impedance reverb tank. An 8BB2C1B might be an obvious choice if the latter tactic is used. Its drive coil has 538 turns and an impedance of 190 ohms at 1 kHz. To drive it fully at 1 kHz requires
![]()
Note however, that the tanks require 44 mA and 56 mA respectively to drive to peak level. Therefore a high-current op amp of some sort is required. I've found that an OPA551 works very nicely and can also take supplies up to ± 30 volts for those who want extra headroom or who are amplifying signals with more high-frequency content.
If you would like to use the 8BB2C1B tank, the drive-circuit component values can be changed to the following:
R1 = 56 ohms
R2 = 1.6k
C1 = 20 uF
C2 = .033 uF
The attentive reader will note that the requirements discussed above were for an undistorted guitar. If a heavily distorted guitar signal is fed into the reverb tank, the amount of drive voltage required will increase substantially, because the clipped guitar signal contains much more power at higher frequencies. Interestingly enough, not being able to reproduce the hard edges of a clipped guitar signal doesn't sound objectionable to my ears. It just means that the reverb part of the amplifier's output will sound a bit softer and less distorted than the main signal. I kind of like that, but another listener may not.
Signal-Recovery Amp
The most basic decision for this stage is whether to use an inverting or noninverting topology. The noninverting topology shown below is preferred because it allows the values of the gain-setting resistors to be optimized for lowest noise while allowing the input resistance of the stage to be set independently.
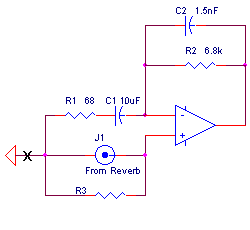
The schematic above shows all the necessary circuit elements. Resistors R1 and R2 set the gain of the stage. The requisite gain will depend on the rest of the system's gain, but gains between 50 and 100 are common. The test circuit uses a gain of 101, with R1 set at 68 ohms and R2 set at 6.8 kohms. The value of C1 is chosen to roll off the low-frequency gain of the circuit. The test circuit uses a 10 m F capacitor, producing a 3 dB point of about 230 Hz. There is considerable leeway in the selection of the 3 dB point-let your ears be the guide. C2, which is 1500 pF in the test circuit, and R2 form a low-pass filter at 15.6 kHz; with such high gain, it is a good idea to keep possible out-of-band noise from subsequent stages.
The inductance of the reverb unit's pick-up coil will resonate with the capacitance of the coil's winding plus the capacitance of the shielded cable used to connect the coil to the circuit. In the case of the 8DB2C1B unit, a short cable will produce a resonance above 20 kHz, and R3 is not needed. For other units, or if a long cable is used, the resonance can move into the audible range. R3 can be used to damp this resonance. Its value can be calculated using the equation presented earlier for determining Q. Alternatively, it may be easier to determine its value empirically by checking for an impedance peak.
Some designs call for placing a capacitor across the reverb unit's output to purposely place the resonance at some audible frequency. Although this technique does produce more output at resonance, it does so at the expense of raising the input impedance at that frequency. In my experience, any increase in output is more than offset by an increase in noise. In addition, the response emphasis is not pleasant to this author's ears. For lowest noise, it is best to damp any in-band resonance with R3.
The most important consideration for the design of this stage is low noise. As previously stated, the stage needs quite a bit of gain. As we did for the drive circuit, let's investigate all the noise sources. First, the Johnson noise of the reverb unit's output coil is connected directly to the stage's input and will be amplified along with the signal. The 8DB2C1B has an output resistance of 200 ohms. The Johnson noise of this resistance is 1.8 nV/rt. Hz. In the test circuit, this resistance will cause output noise of 181 nV/rt. Hz.
The Johnson noise of R1 will be amplified by the R2/R1 ratio. Therefore, R1 must be kept smaller than the resistance of the reverb coil if it is not to add appreciable noise. Because noise sources add in an r.s.s. (root sum squared) way, if R1 is less than one-third the value of the reverb coil's resistance, the noise it will add will increase the total noise by less than 1 dB. The 68 ohm resistor used in the test circuit meets this criterion. Note, however, that some resistors have noise considerably in excess of Johnson noise. Carbon composition units are notorious in this regard and therefore shouldn't be the first choice for R1. The Johnson noise of R2, because it is not amplified, is negligible.
Because impedance at the noninverting node of the op amp is low, op amp current noise at this input causes negligible output noise. Current noise at the inverting input is multiplied by the value of R2. Still, this noise source will also be negligible, even for a bipolar-input op amp. Finally, the op amp's voltage noise is amplified along with its signal. Unless one uses a very quiet amp, this noise will be higher than the Johnson noise of the reverb coil, and so will be the dominant noise source of the stage. If an op amp with an input-referenced voltage noise 5 nV/rt. Hz is used, the total output noise of the stage is about 540 nV/rt. Hz. Over a 10 kHz bandwidth, total noise is about 60 mV r.m.s., quite a respectable figure.
In many designs, the reverb unit is attached so it does not electrically contact the amplifier's chassis. As such, no ground loops will be produced. If, however, the reverb unit electrically contacts the chassis, the ground connection at the op amp input may have to be eliminated to avoid hum. If so required, break the connection marked with an "x" in the schematic.
Follow these simple design guidelines:
Conclusions
The test circuits have been auditioned by several guitarists, all of whom have pronounced the quality of the reverb to be excellent. I have seen many statements that claim that op amps should not be used for interfacing to spring reverbs because they are too noisy or are unsuitable in some other way. I can only assume that such statements are based on misconceptions or poor circuit design. I believe that this tech note shows conclusively that op amps provide a nearly ideal mate to a spring reverb. In the combination of performance, size, and cost, no other circuit element can do such a superb job.